
Attention PSLE 2025 Parents and Students!
Did you know that speed-related word problems will be officially removed from the PSLE syllabus starting in 2026? That means this year's cohort is the final batch to face speed, distance, and time questions in the PSLE exam. However, with many tuition centres no longer covering this topic, parents are now urgently searching for effective and reliable ways to help their children master this concept before the big day.
In this article, we'd break down 4 Proven Singapore Maths problem-solving methods for tackling speed questions.
Each method comes with its own advantages and limitations, and we'll explain which works best for different learning styles.
If you're looking for a last-minute speed problem crash course for PSLE 2025, or simply want to future-proof your child's problem-solving skills with smart, exam-tested techniques, this guide is for you!
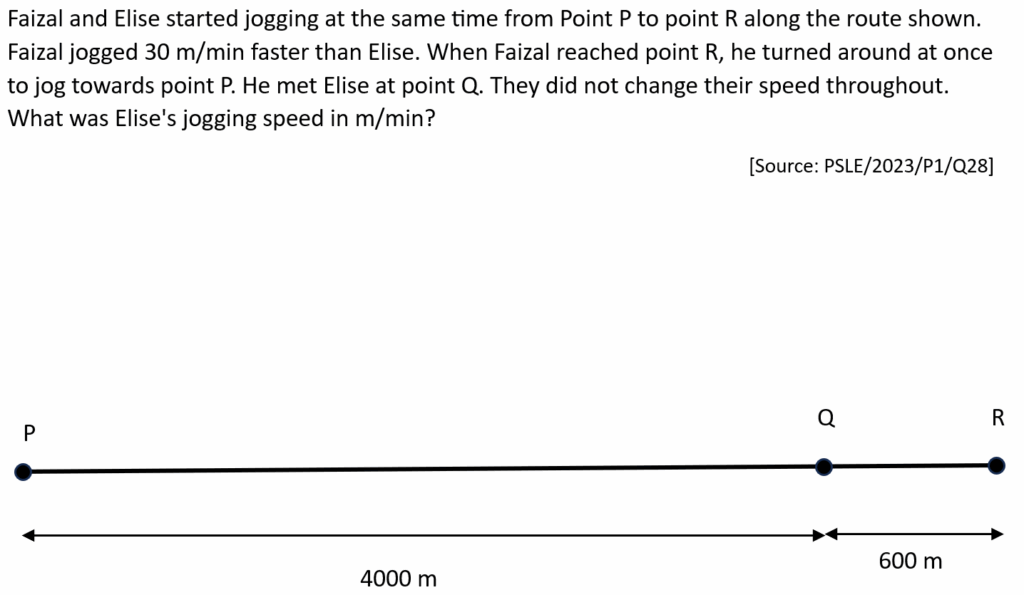
Centre A Method (A for Algebra)
This approach uses algebra, typically introduced at the secondary school level. It involves setting variables for speed and solving equations.
Let v be Elise's speed in m/min,
v × t = (v + 30) × t – 2 × 600
vt = vt + 30t –1200
30t = 1200
t = 40min
v = 4000 ÷ 40 = 100 m/min
Answer: Elise's jogging speed is 100m/min.
Advantages:
Limitations:
Centre B Method (B for Brief)
This method presents a very stripped-down, shortcut-based solution to the problem:
2 × 600 = 1200
1200 ÷ 30 = 40
4000 ÷ 40 = 100
Answer: Elise's jogging speed is 100 m/min.
Advantages:
Risks:
Centre C Method (C for Concise)
This method directly links distance and speed ratios:
Distance (Faizal) → 4000 + 600 + 600 = 5200 m
Distance (Elise) → 4000m
Distance (Faizal) : Distance (Elise)
5200 : 4000
13 : 10
Speed (Faizal) : Speed (Elise)
13 : 10
Difference (speed) → 13 – 10 = 3 units
→ 30 m/min
3 units → 30 m/min
1 unit → 30 ÷ 3 = 10 m/min
10units → 10 × 10 = 100 m/min
Answer: Elise's jogging speed is 100 m/min.
Centre D Method (D for Detailed)
A step-by-step breakdown, including variables, diagrams and distance-time relationships.
Let
‒ v be Elise's constant jogging speed in m/min,
‒ so that Faizal's constant jogging speed is v + 30 m/min.
From the diagram (and question text), when they meet at point Q, Elise has already covered 4000 m from P. Meanwhile, Faizal must have run all the way to R (which is 4600 m from P), turned immediately, and come back until he meets Elise at 4000 m. In other words, Faizal's total jogging distance by the time of meeting is:
4600 (P → R) + (4600 − 4000) (R → Q) = 4600 + 600 = 5200 m
Elise's distance at the meeting is exactly 4000 m. Hence by the time they meet:
(Faizal's distance) − (Elise's distance) = 5200 − 4000 = 1200 m
But note also that they both start together at P and jog without changing speed. Let t minutes be the time elapsed from the start until they meet at Q. Then:
Since Faizal has gone 1200 m farther than Elise by that meeting moment, we have:
(v + 30)t − v t = 1200
30 t = 1200
t = 40 min
Thus, in 40 min, Elise covers 4000 m. Therefore, her speed is:
v = distance ÷ time = 4000 ÷ 40 = 100 m/min
Answer: Elise's jogging speed is 100 m/min.
Advantages:
Risks:
Conclusion
With speed questions making their final appearance in PSLE 2025, now's the time to equip your child with effective, exam-smart problem-solving strategies. Among the available methods, the Bamboo Path Academy's ratio method remains a clear, reliable and intuitive approach for tackling speed, distance and time questions confidently.
Support your child's PSLE success with Bamboo Path Academy
At Bamboo Path Academy, we specialise in PSLE Math preparation and offer targeted crash courses and problem-solving workshops for key topics like speed questions before the syllabus changes.
Contact us via our Contact form, Whatsapp or Email to learn more or to book a free diagnostic session today!
